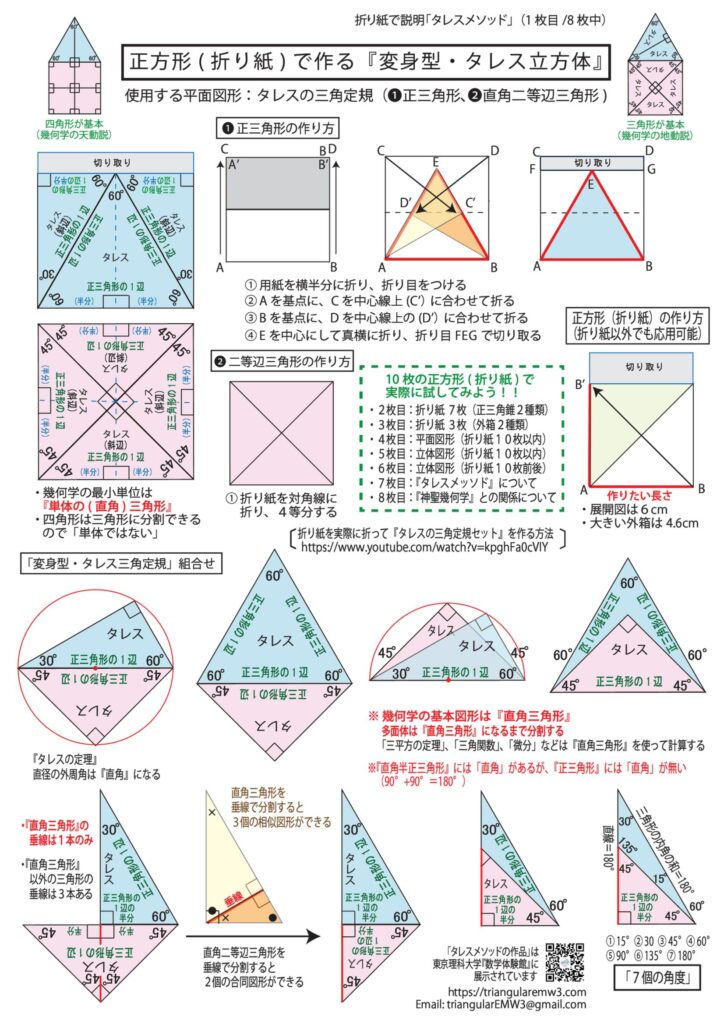
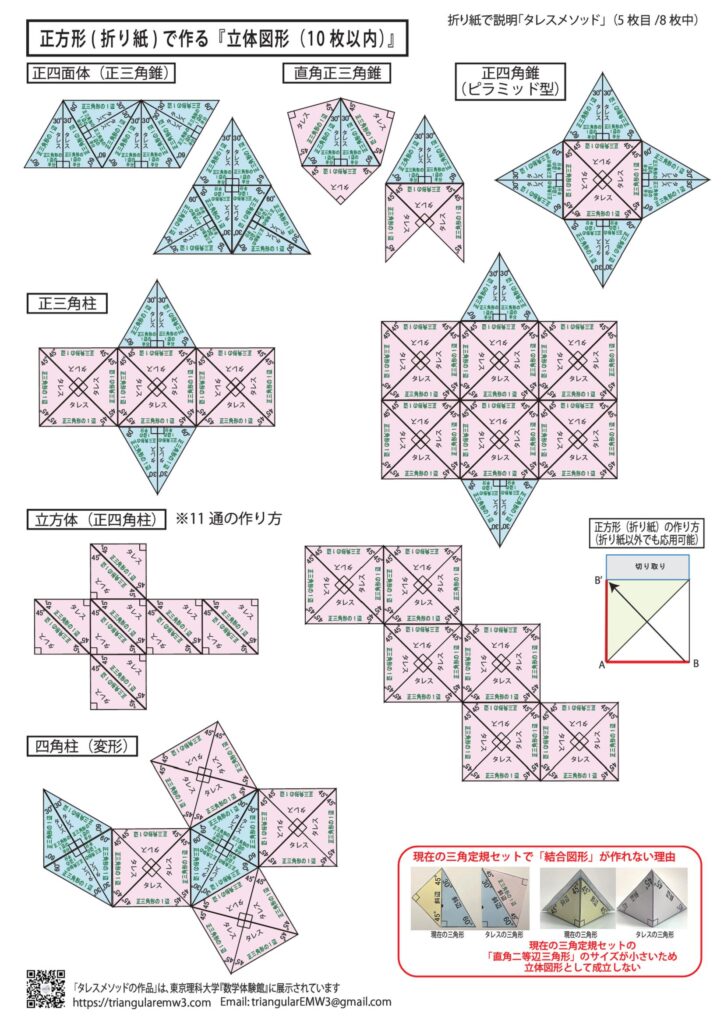
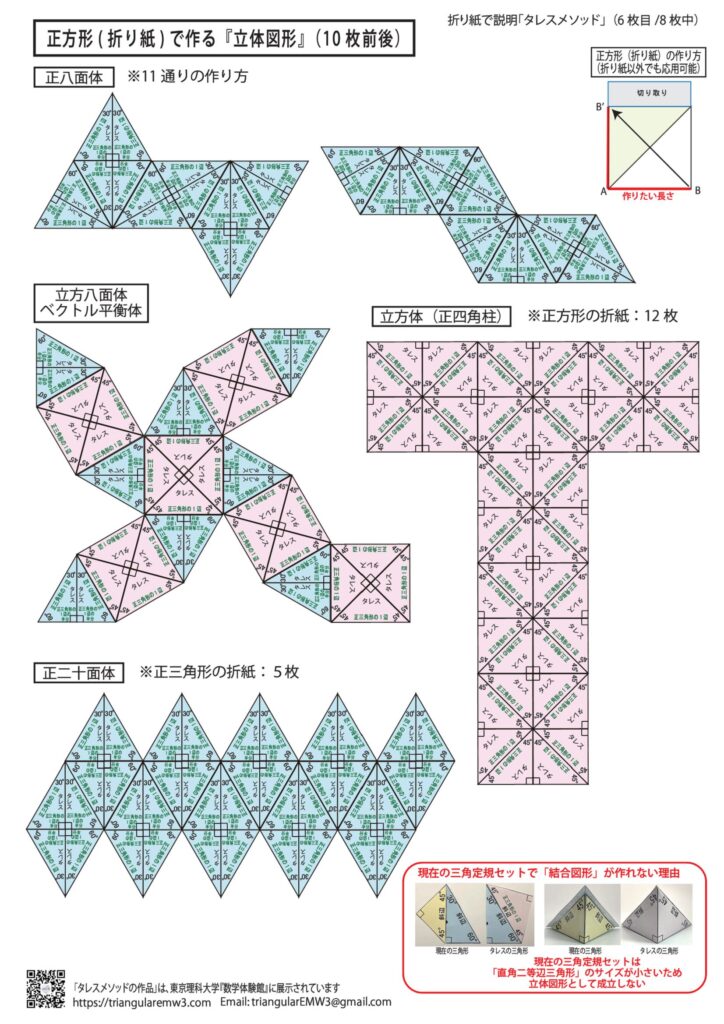
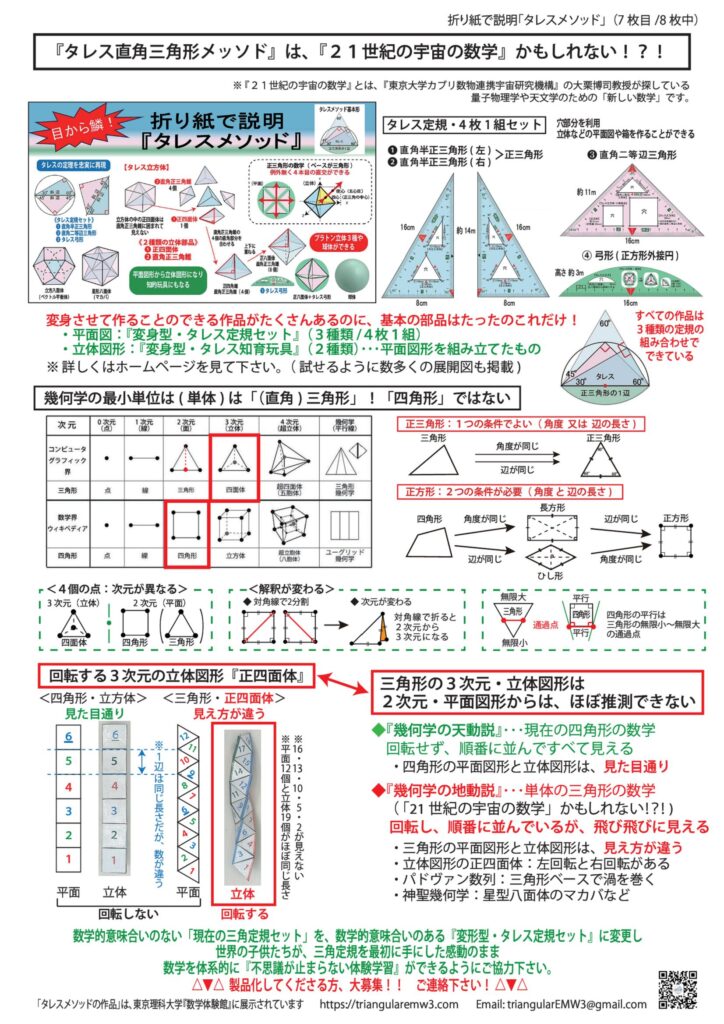
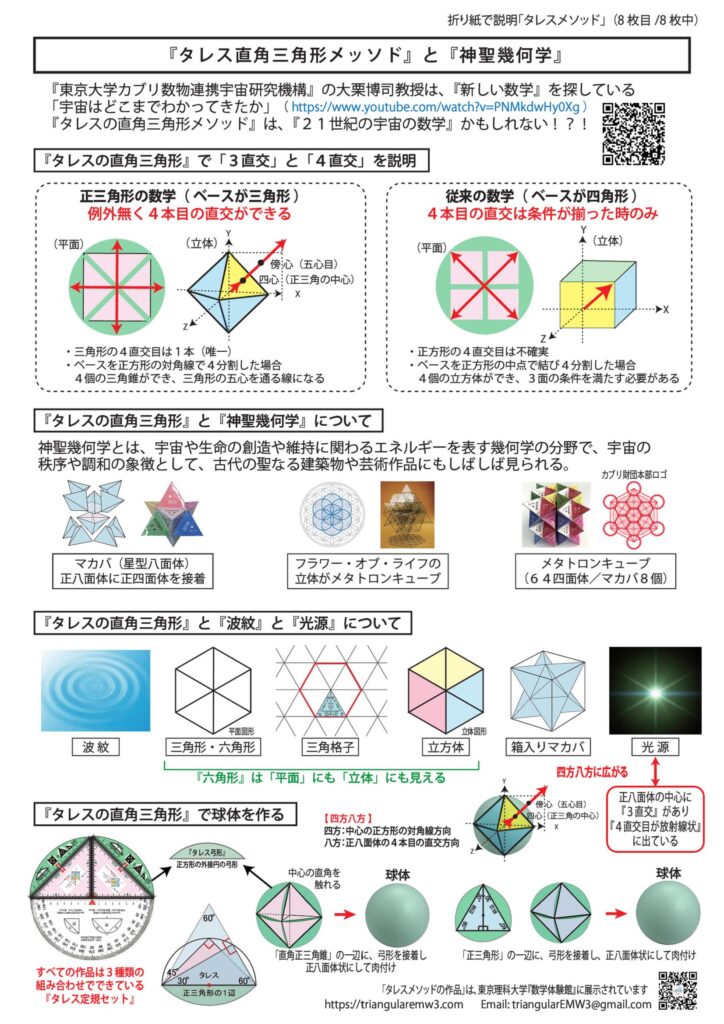
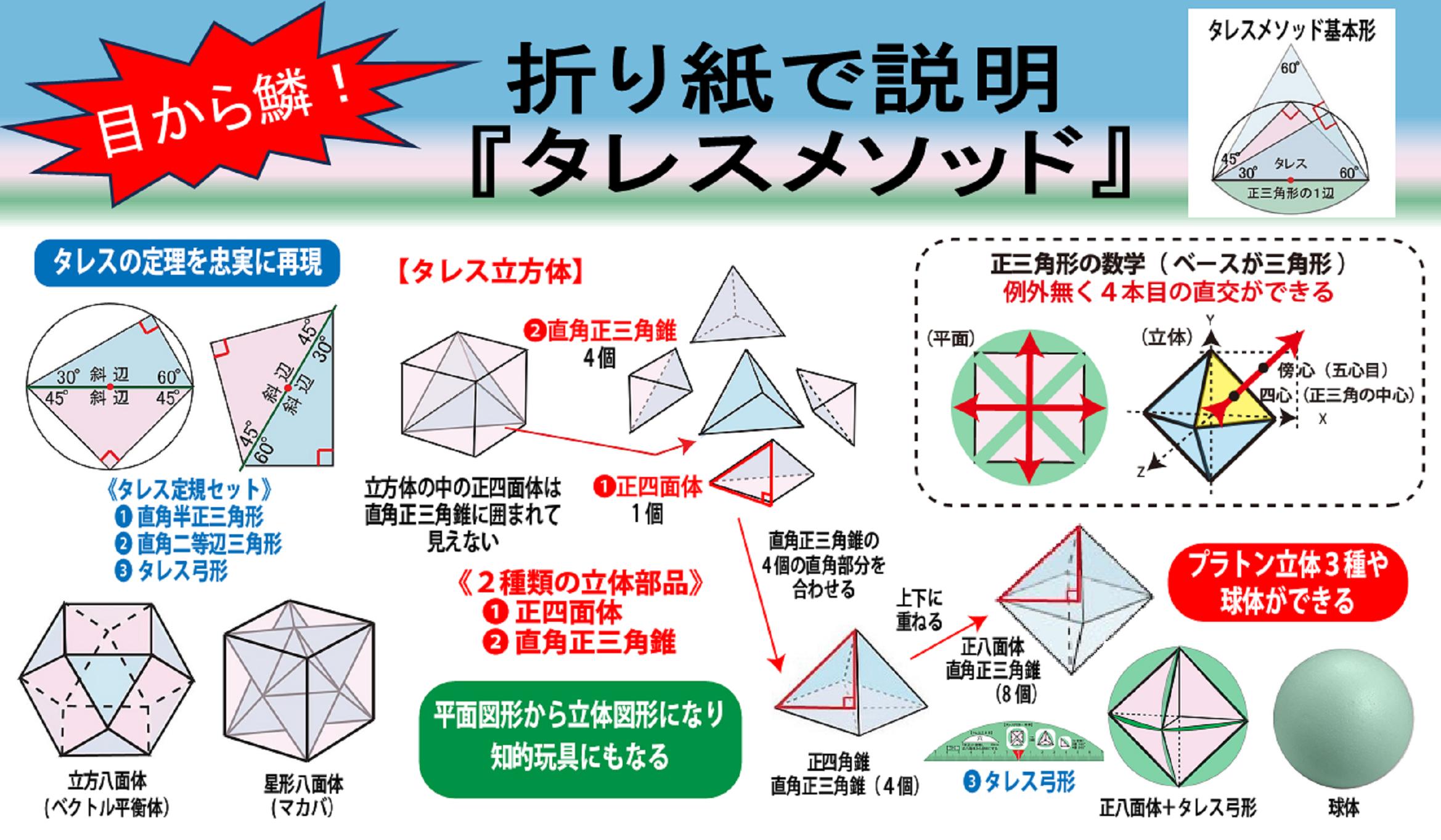
●『タレスの直角三角形メソッド』を正方形の『折り紙』を使って説明しています
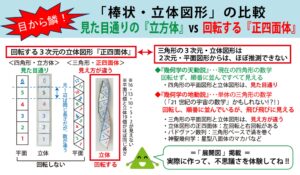
●『幾何学の地動説』とも言える、奇想天外な『幾何学の単体:三角形』の不思議
●「展開図」を組み立てて、ご自身で『目から鱗』の体験をして下さい
※広く普及することを願い、作品のデータや展開図など無料で提供していますが、著作権は放棄しておりません
※実用新案登録済
【問い合わせ】
1枚目:『タレス三角定規』の作り方と『タレスの定理』についての説明
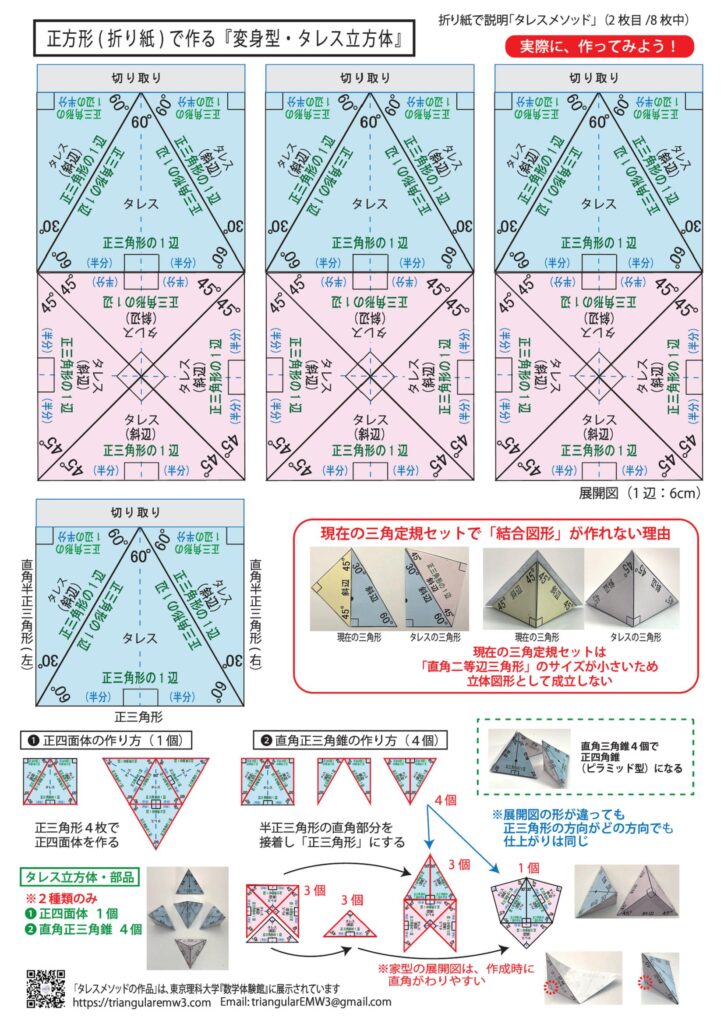
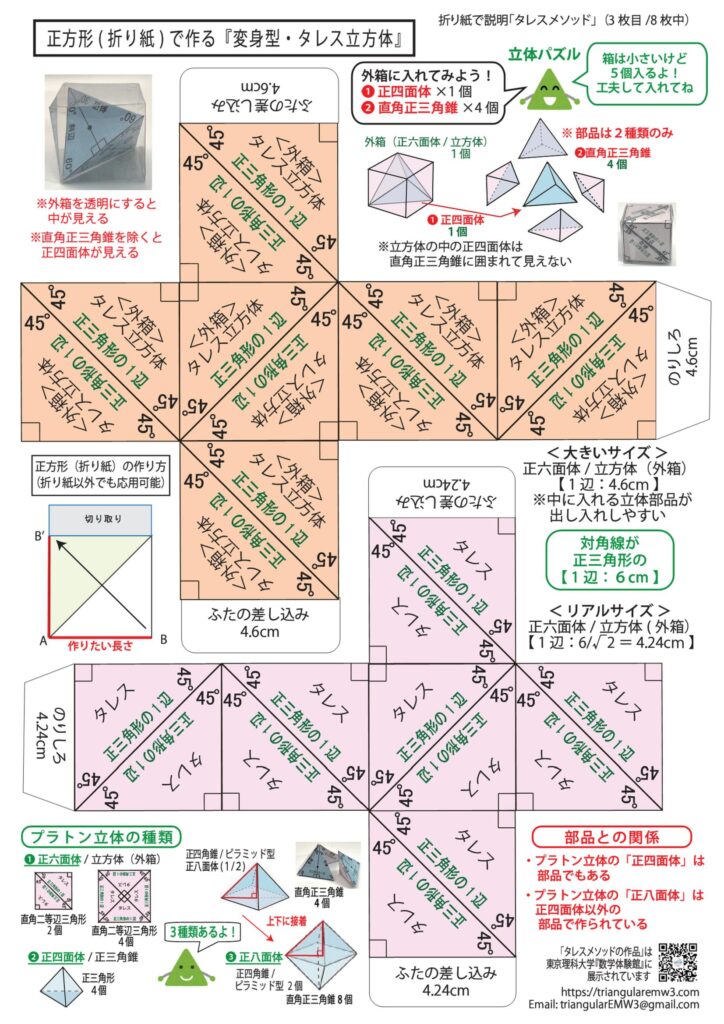
2枚目~3枚目:折り紙の展開図(1辺6cm)、実際に作ることができます
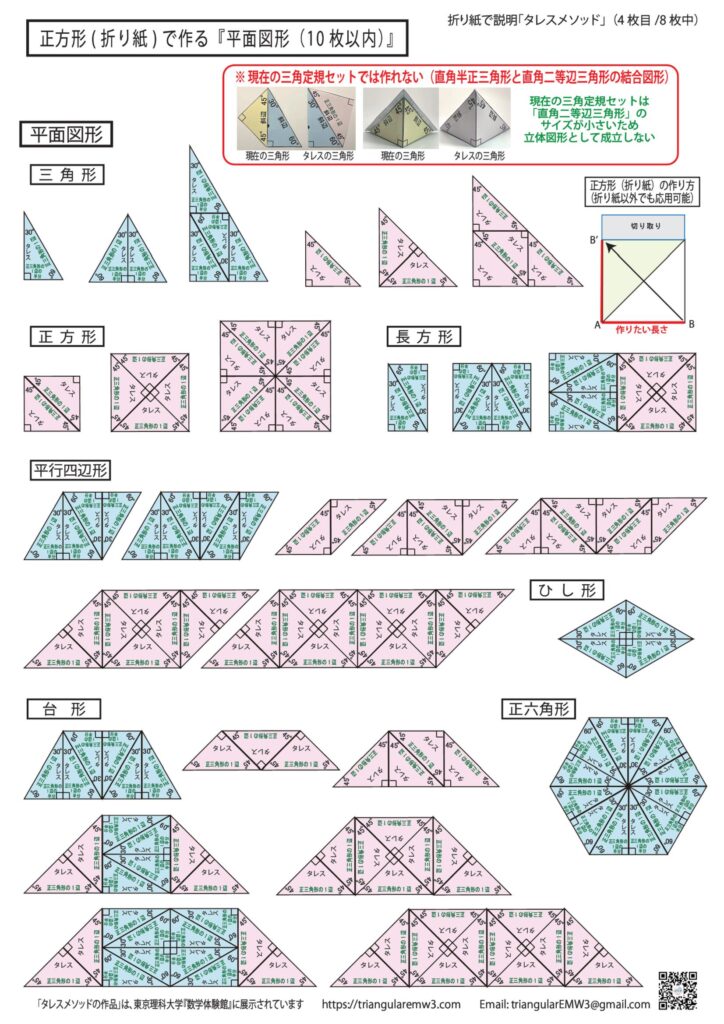
4枚目~6枚目:平面図形、平面図形から立体図形の展開図、
※2種類の結合は『タレス三角定規』だからできる(可能)
※現在の三角定規では結合することはできない(不可能)
7枚目:『タレスの直角三角形メソッド』について
8枚目:『神聖幾何学』との関係について