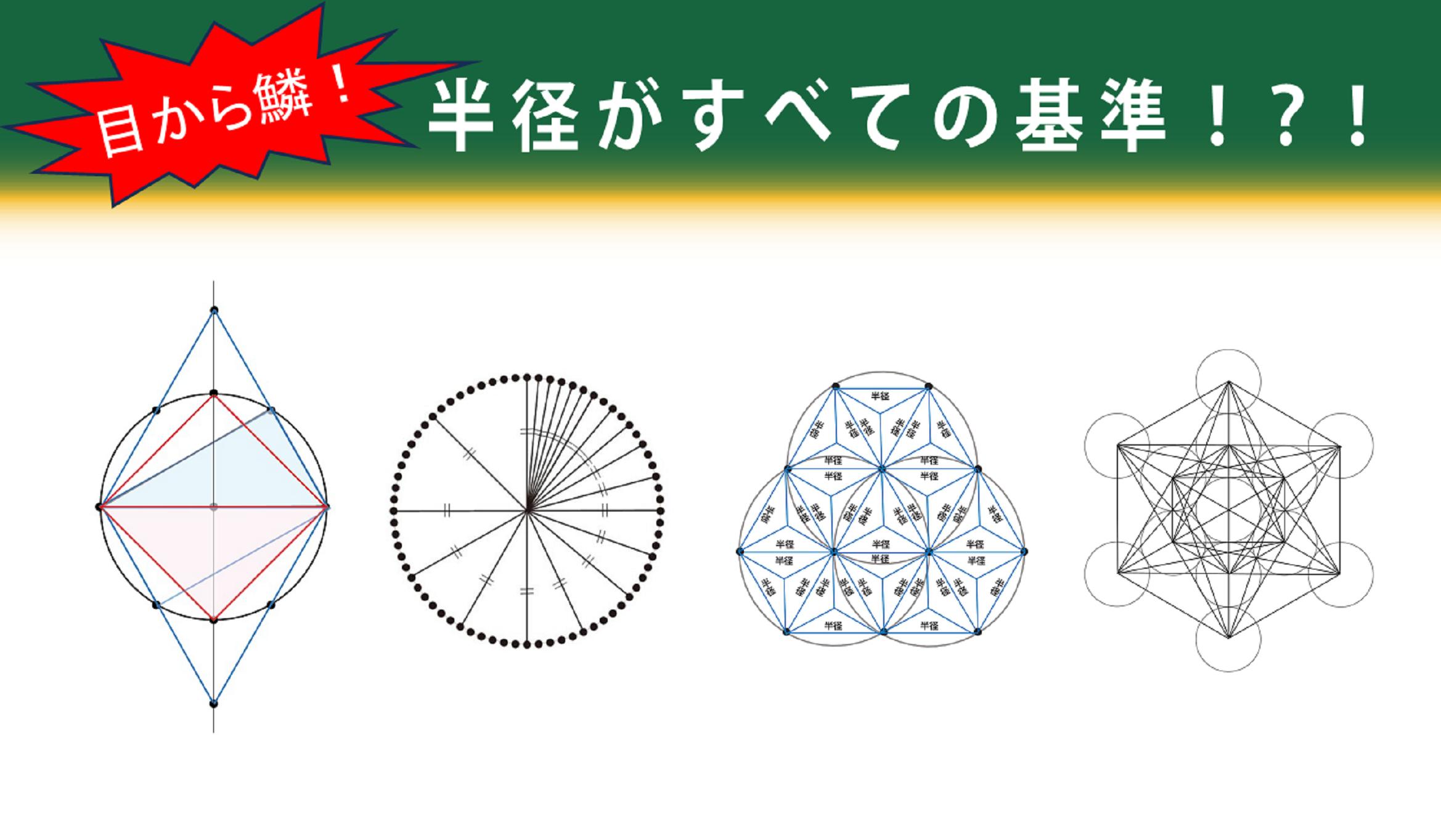
半径は、コンパスで円を書く時に決める長さである。
一旦、この「半径＝長さ」が決まると、この長さで円が描かれ、直線が引かれ、プラトン立体を始めとする幾何学ができる。
きっかけについて
ナオキマンのYOUTUBE
『宇宙の法則・３・６・９が意味するものとは・・・』
あなたが、３，、６，９という数字の素晴らしさを知れば
宇宙への鍵をてにすることになる ＝ニコラ・テスラ＝
https://www.youtube.com/watch?v=CYaHFYua-oE&t=4s
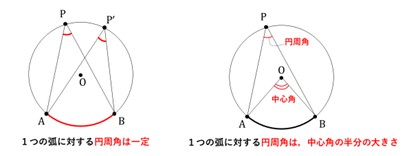
タレスの定理
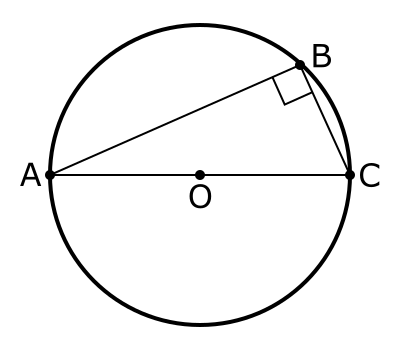
世界最古級の幾何学の定理
直径の円周角は、必ず直角になる
＜幾何学の５定理＞
１．円は中心点を通る直線で二等分される。
２．二等辺三角形の両底角は等しい
３．交差する直線の対頂角は等しい
４．三角形は底辺と両底角で定められる
５．半円に内接する三角形は直角三角形である
※三角形の内角の和は２直角＝１８０度
タレス：古代ギリシア（紀元前６世紀）の記録に残る最古の（自然）哲学者
古代ギリシア７賢人の一人
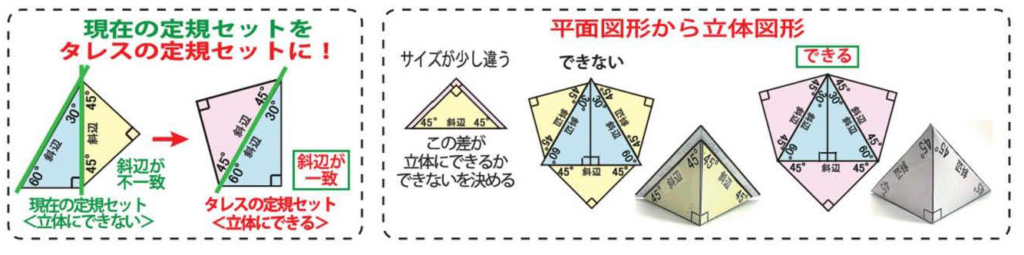
三角定規セットについて
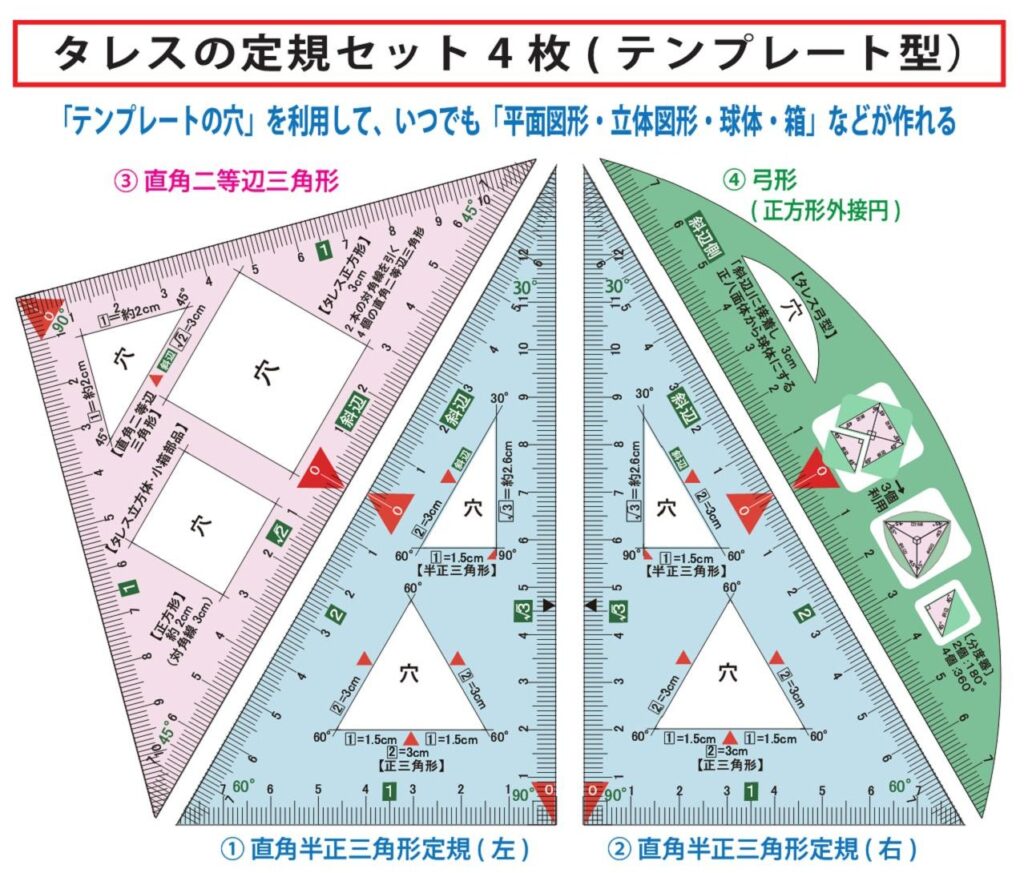
タレスの直角三角形
直角が重要：三角比、三角関数、微分など、計算ができるようになる
直角半正三角形：半正三角形の直角は、正三角形になると消える。長方形になると残る
直角二等辺三角形：直角二等辺三角形の直角は消えても、45度+45度＝90度となり、新たな直角が現れる
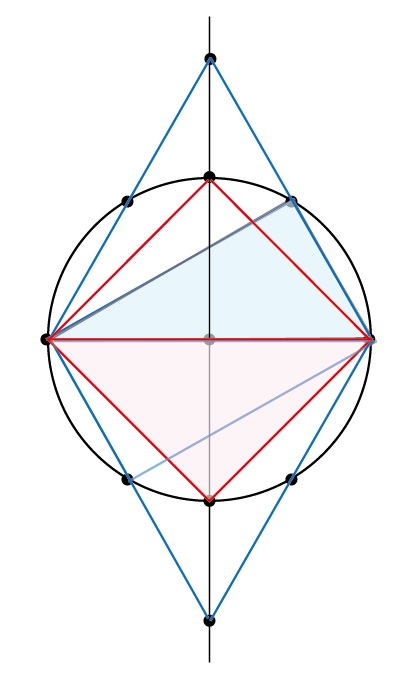
『タレスの直角三角形』
円の直径の外周角は
必ず、直角になる
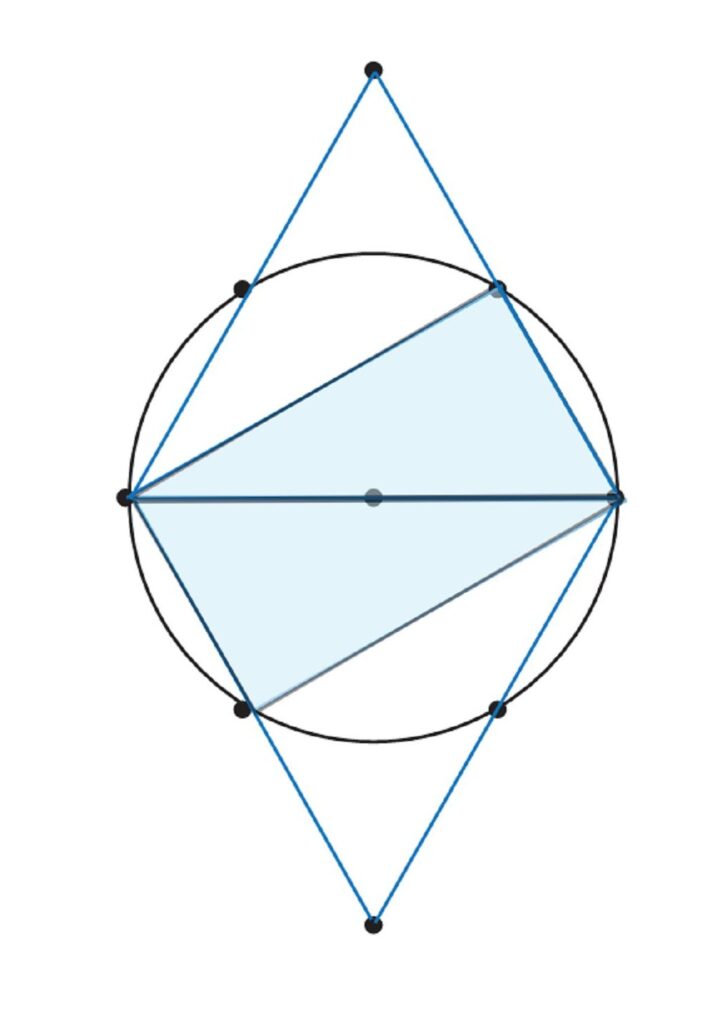
30度・60度・90度の直角三角形
長方形ができる
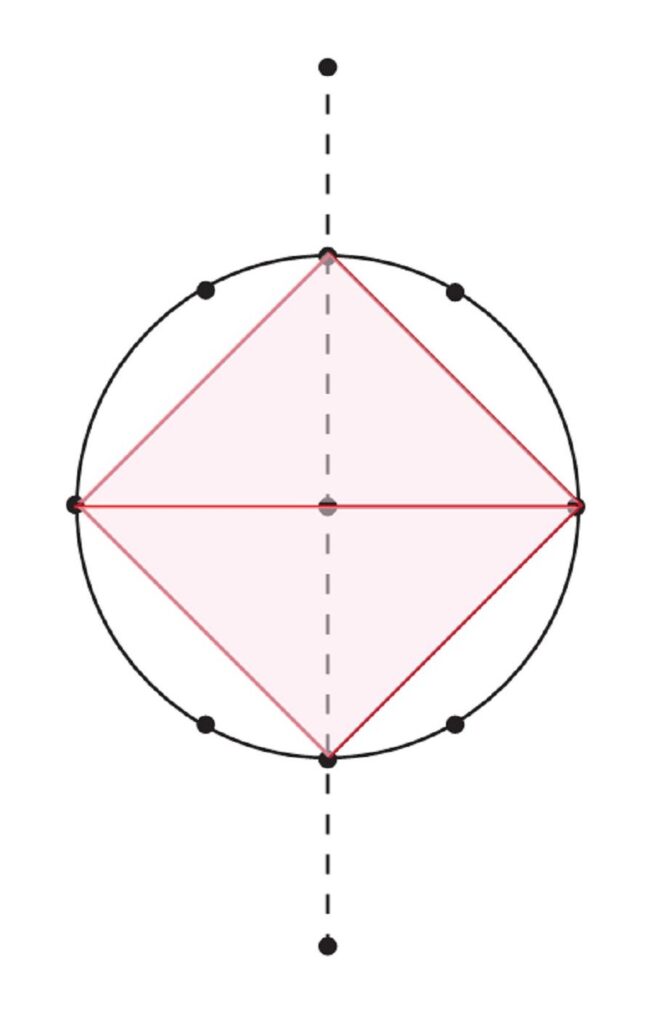
45度・45度・90度の直角三角形
正方形ができる
【動画】『半径』で作る「タレスの直角三角形」
次元について
幾何学の最小単位（単体）は、「三角形」であり、「四角形」ではない！
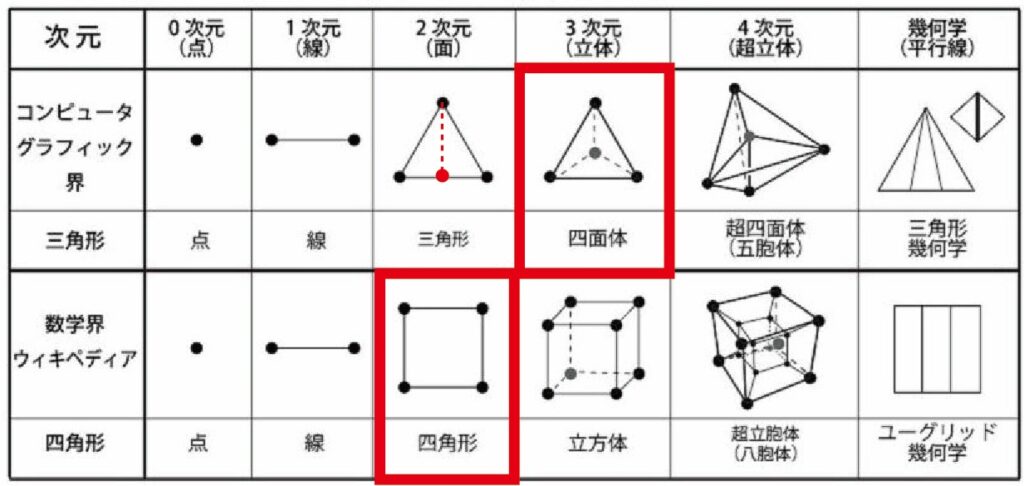
各次元の説明
０次元：点
点（中心）
ある１点を決める
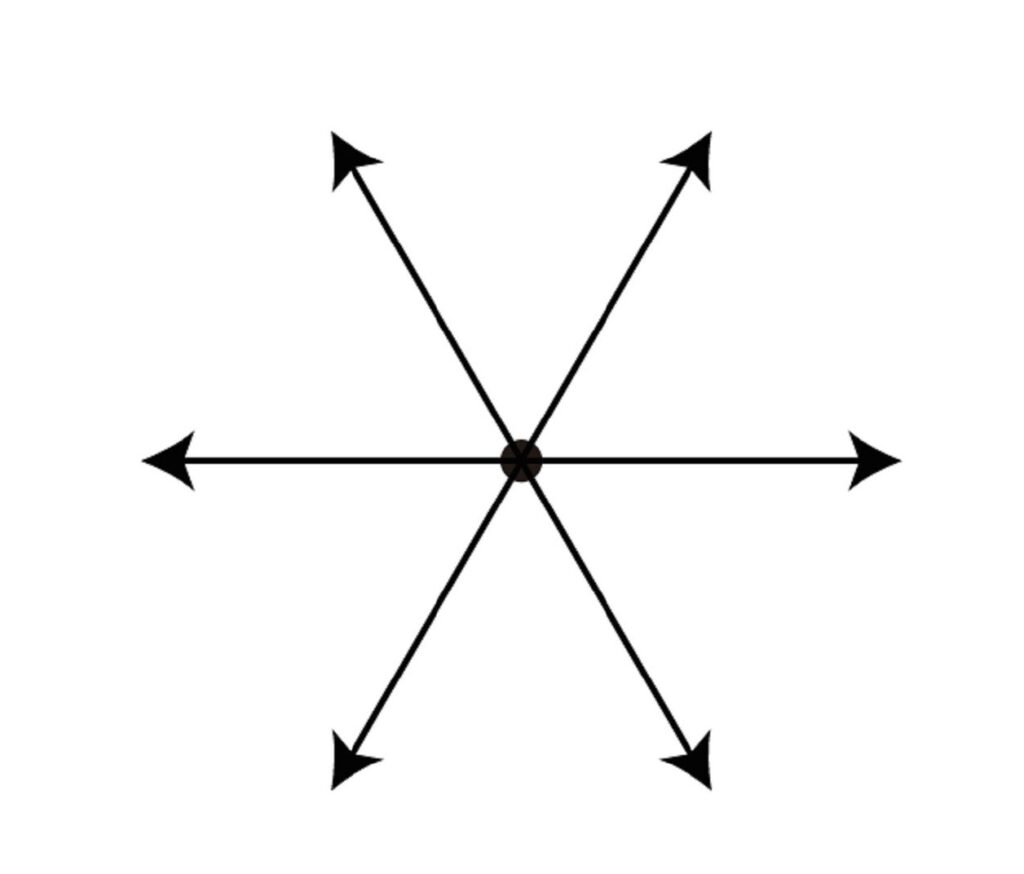
中心からあらゆる方向に放射
波紋の様に広がるイメージ
１次元：線
線
１点からある方向に一定の長さが決まる＝１次元の線
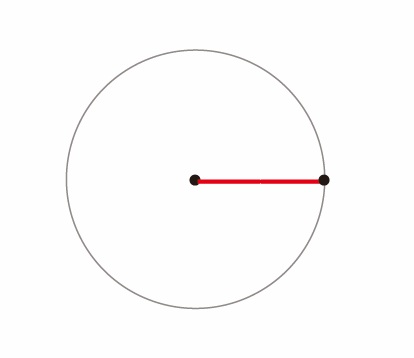
半径
線を半径とした円を描く
これがすべての『基準』となる
２次元：平面
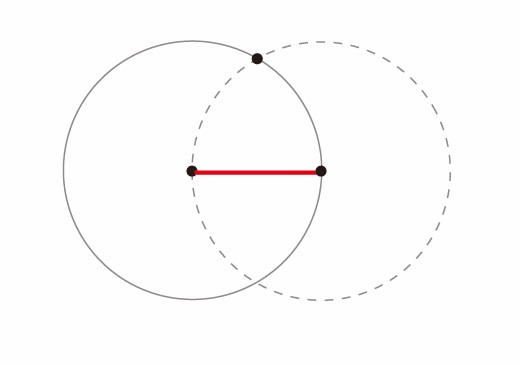
円周の点から半径との交点に印をつける＝もう１つの円の半径にもなる
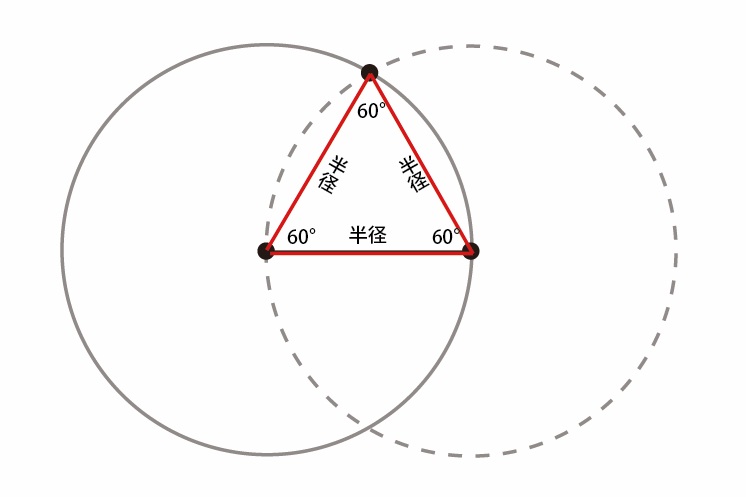
半径を１辺とした正三角形の平面ができる
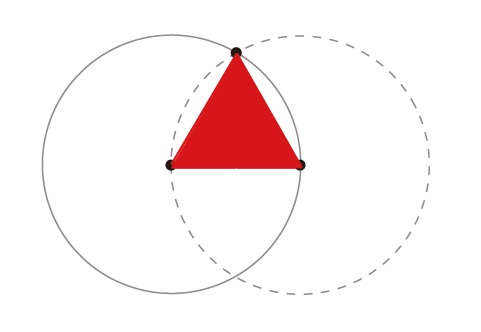
２次元平面：正三角形
３次元：立体
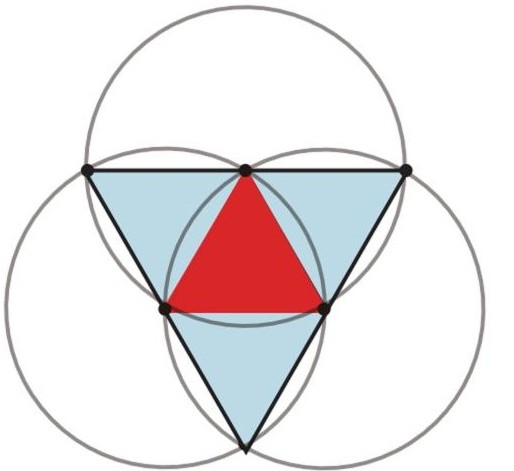
正四面体の展開図
正三角形の３辺に３個の正三角形を配置（合計４個）
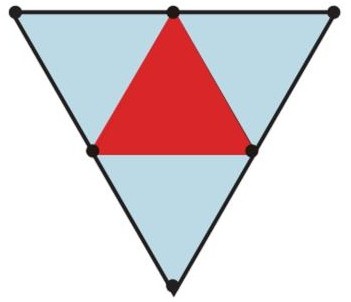
４個の正三角形を接着して正四面体にする
３次元立体：正四面体
４次元：超四面体（五胞体）
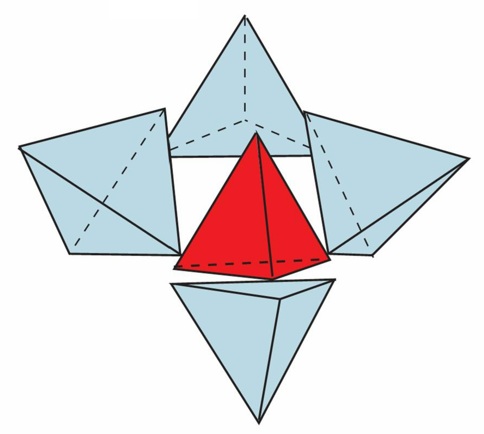
正四面体の４面に４個の正四面体を配置（合計５個）
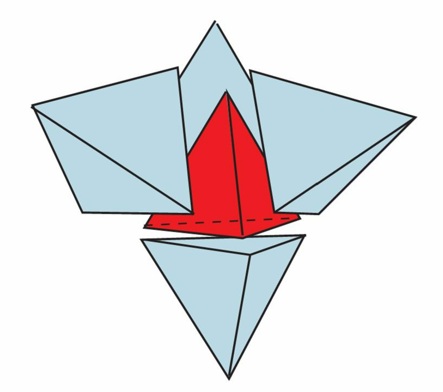
４個の正四面体を接着して、超正四面体（五胞体）にする
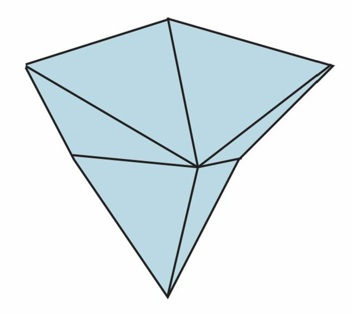
４次元立体：超四面体（五胞体）
正四面体のダビンチの星
半径の長さを基準にして幾何学図形はできている！？！
半径の定義
半径と円の関係
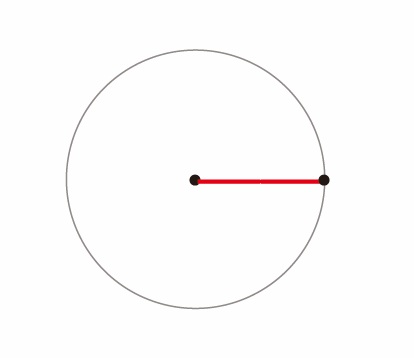
半径と円
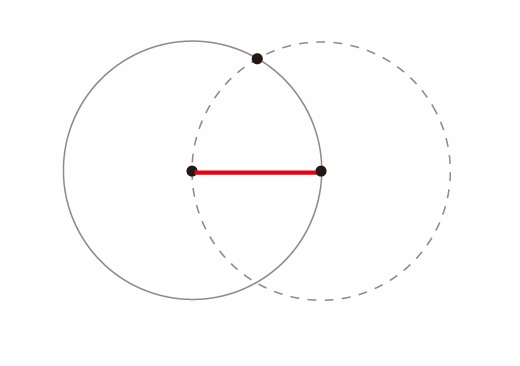
２個の円と半径
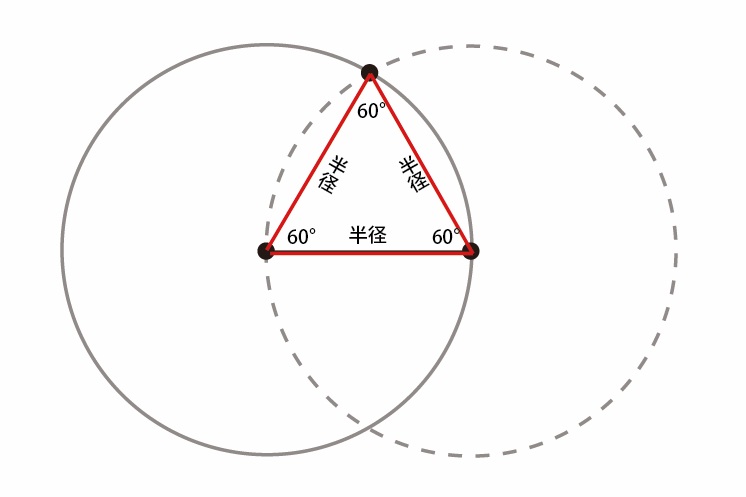
２個の円と半径
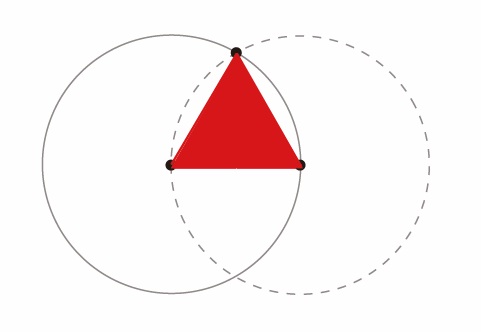
２個の円と正三角形
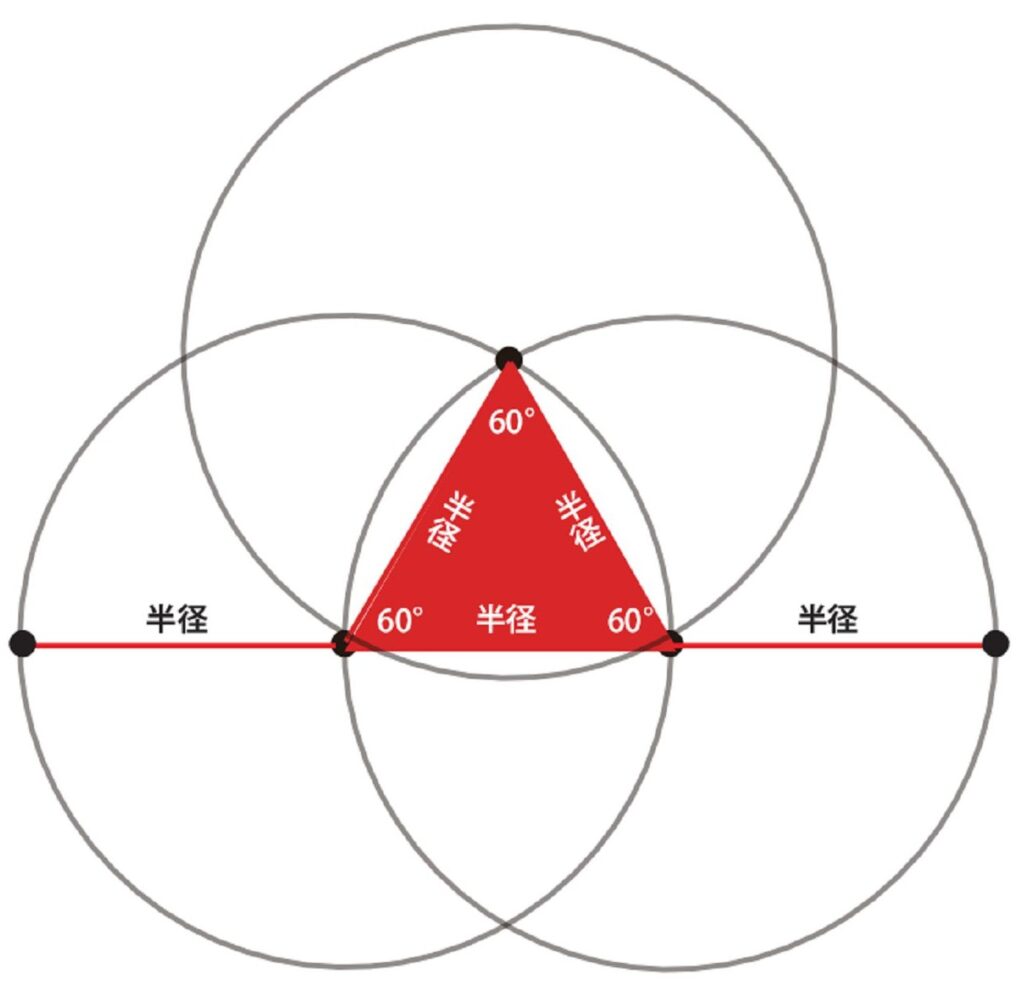
３個の円と正三角形
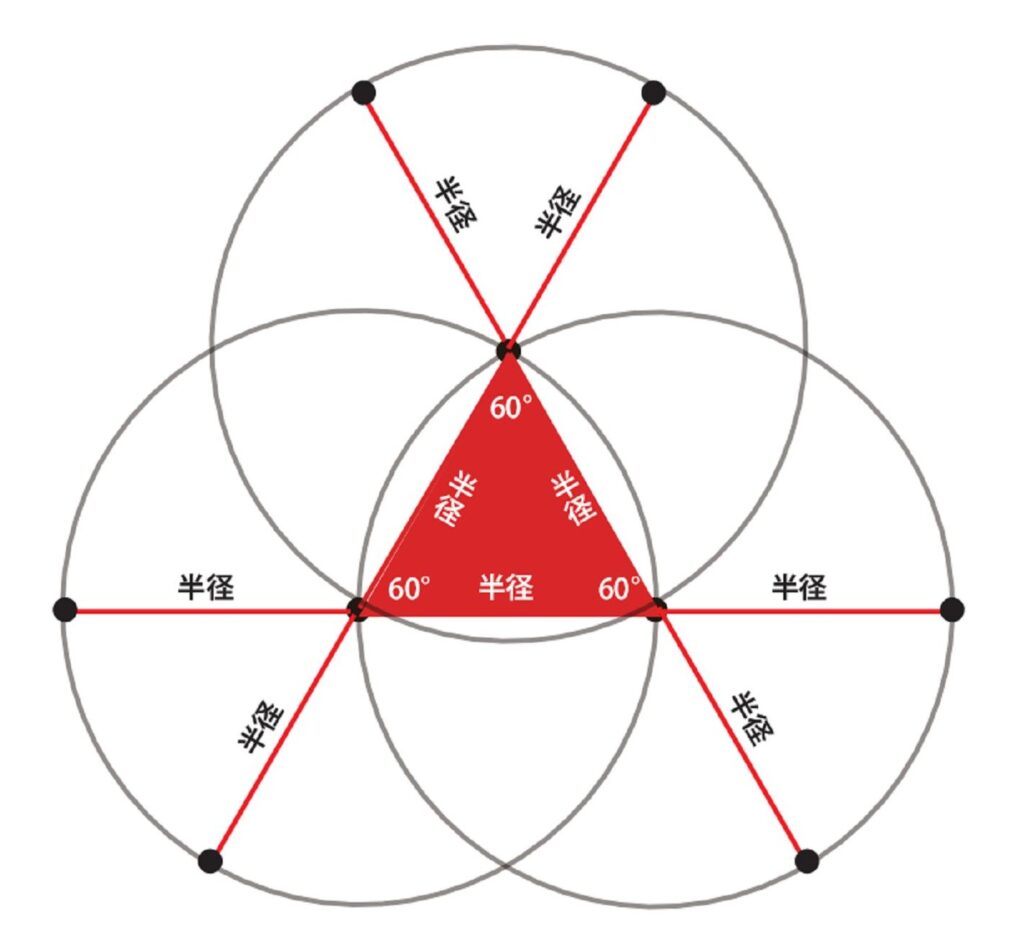
３個の円と正三角形
半径と六角形の関係
半径と六角形・麻の葉との関係
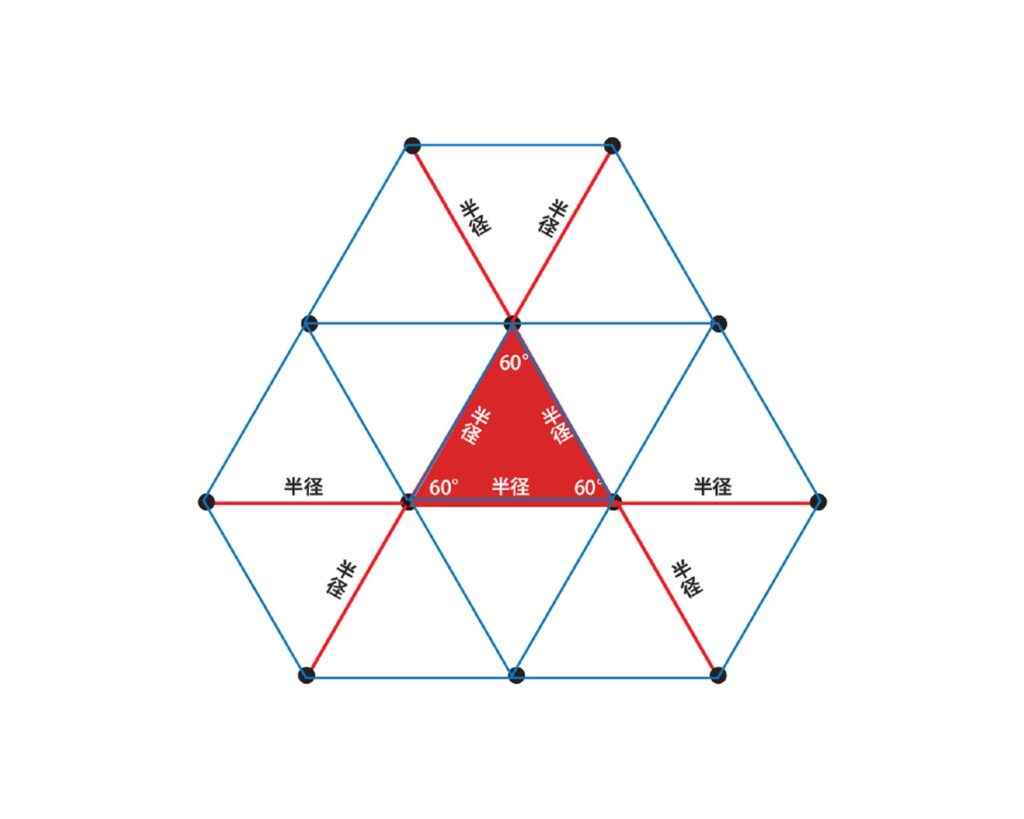
六角形
六角形・麻の葉
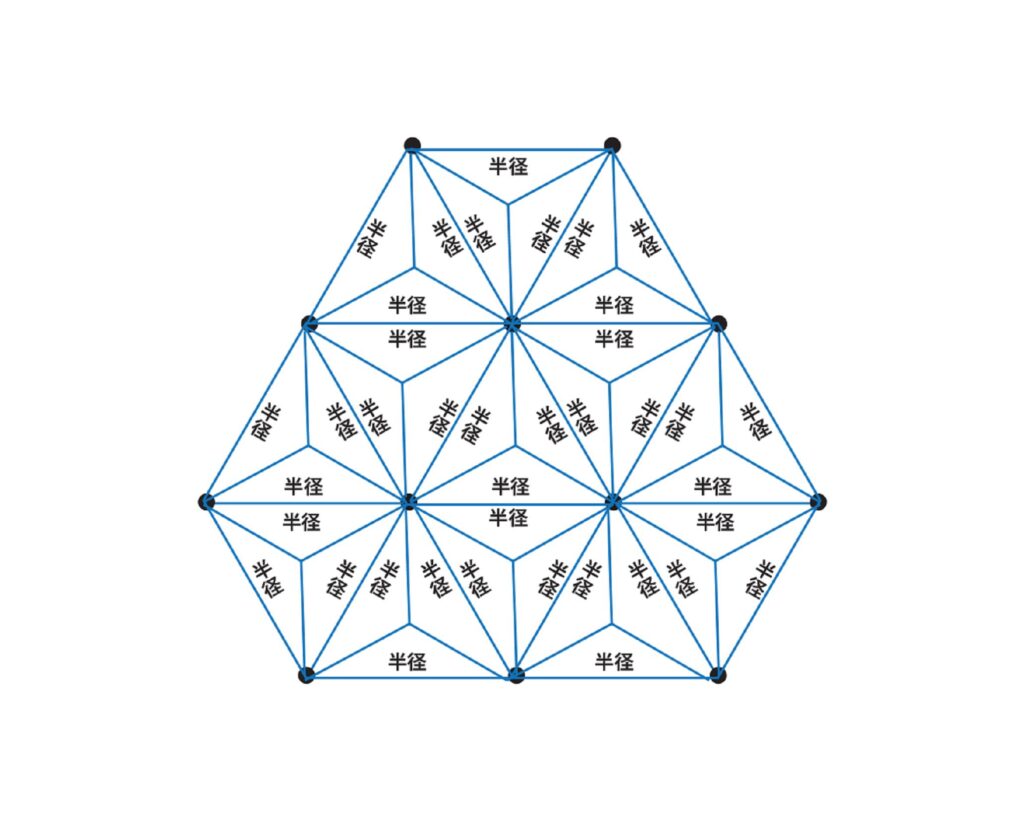
六角形・麻の葉
神聖幾何学模様の１つで、生命の種子や創造のシンボルとして知られている
半径と円・三角形・六角形・麻の葉
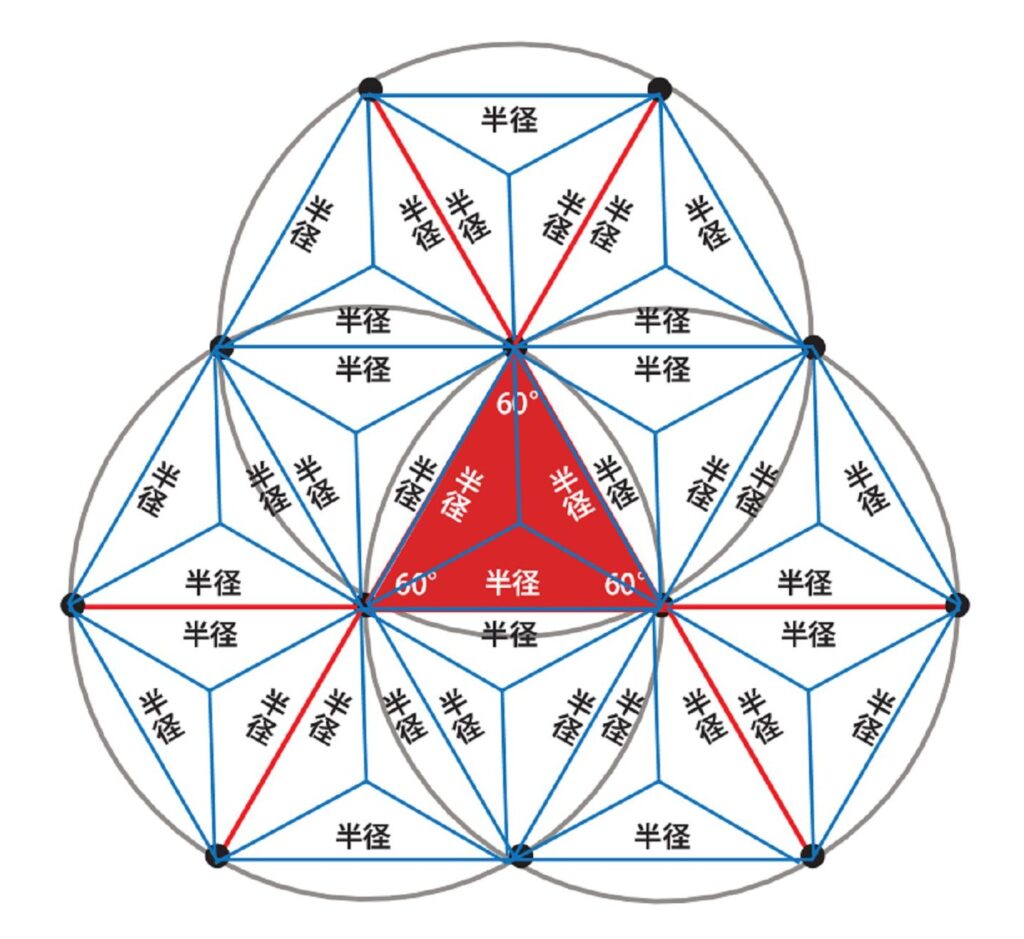
円・六角形・麻の葉
円・六角形・麻の葉
半径と神聖幾何学の関係
シード・オブ・ライフ
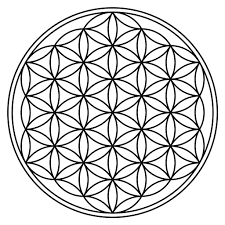
フラワー・オブ・ライフ
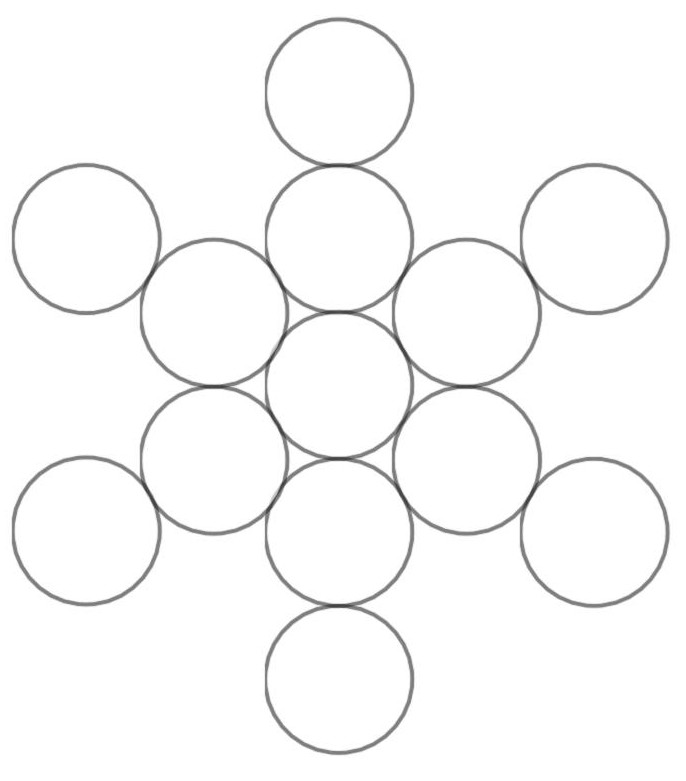
フルーツ・オブ・ライフ
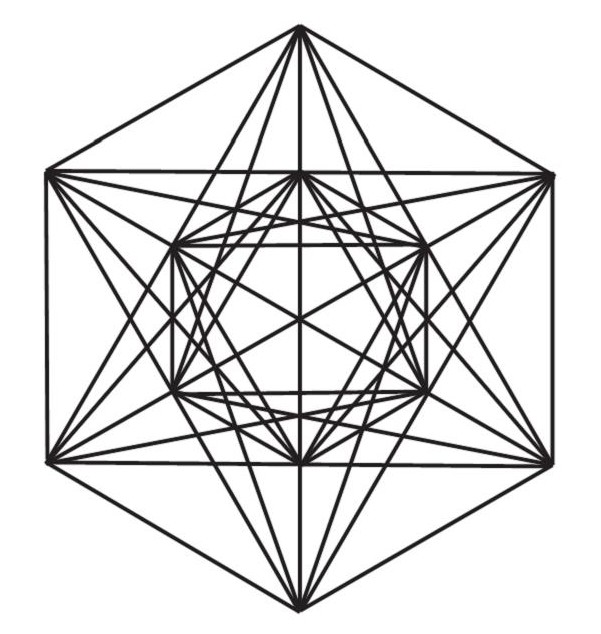
メタトロン・キューブ
（線のみ）
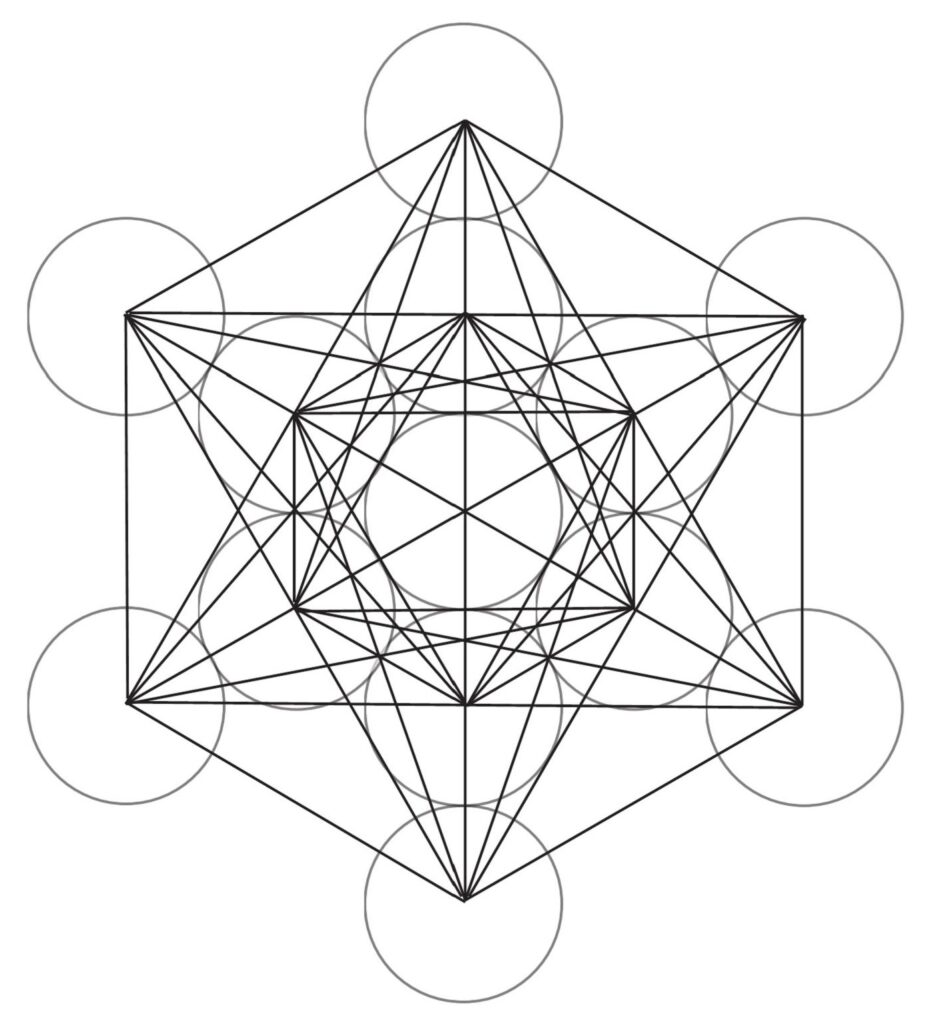
メタトロン・キューブ
神聖幾何学は、コンパスを使って円を描き、交点を線で結んだもの
半径と麻の葉模様
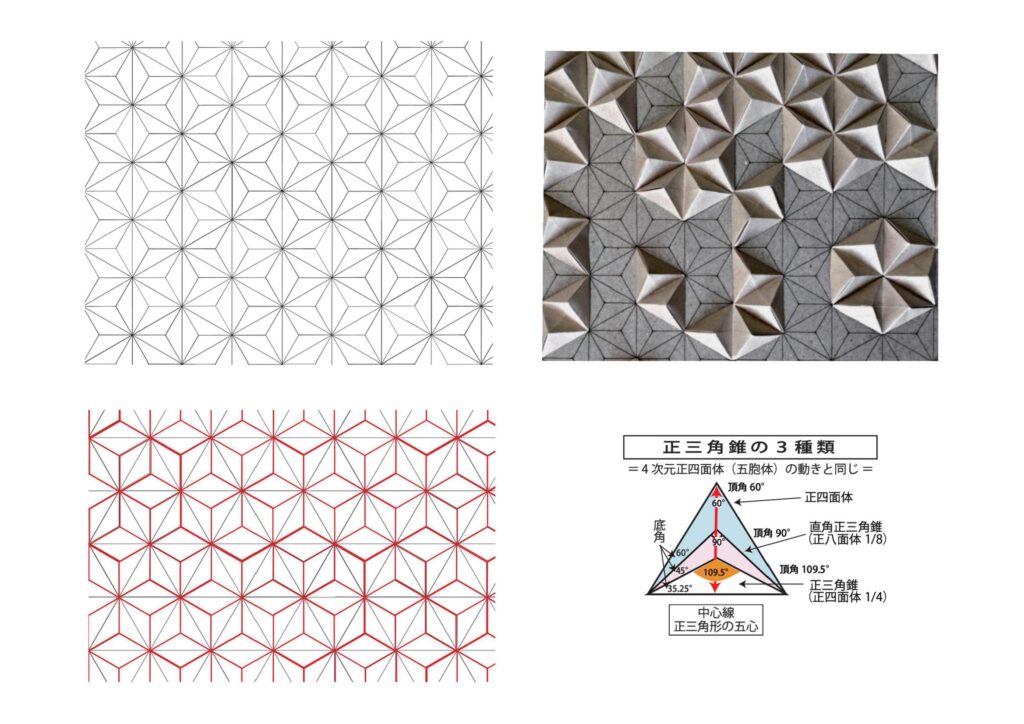
六角形や麻の葉は、見方により立方体にみえる 麻の葉は正三角形の上に三角錐がついている
六角形や麻の葉は、見方により立方体にみえる
麻の葉は正三角形の上に三角錐がついている
底面が三角錐で、高さは自由
上から見るとわからないが、横から見ると違う
